The IBIS telescope is a device based on a coded aperture imaging system. The mask chosen for IBIS is based on a cyclic replication of MURA (Modified Uniformly Redundant Array) of order 53, expanded to 95 pixels. The properties of the MURA patterns are described in the papers [11], [13].
For IBIS, the mask is about 1.8 times larger than the detector. The most important advantage of such configuration is that for a large fraction of the sky a source projects a complete pattern on the detector (the Fully Coded Field Of View, FCFOV). The part of the sky from which only a fraction of the source radiation directed towards the detector plane is modulated is called Partially Coded Field of View (PCFOV). The complete field of view of the telescope (FOV) is therefore composed by the central FCFOV of constant sensitivity and optimum image properties surrounded by the PCFOV of decreasing sensitivity. A source outside the FOV simply contributes to the background level.
Representing the mask with an array of 1 (open elements) and 0 (opaque ones), the detector array will be given by the convolution of the sky image by plus an unmodulated background array term ,
MURA patterns have the remarkable property that their cyclic autocorrelation gives a delta function. The decoding array, , is inverse to where (i.e., = for =1 and = 1 for =0) and thus is correlation inverse.
With the help of array we can reconstruct the sky:
where differs from only by the term, which for a flat array is a constant level that can be measured and removed.
To have a sidelobe-free response a source must be able to cast a whole basic pattern on the detector (fully coded source). To make use of all the detector area and to allow more than one source to be fully coded, the mask basic pattern is normally taken as the same size and shape of the detector and the total mask made by a cyclic repetition ( 2 2 for rectangular mask) of the basic pattern. For such optimum systems a FCFOV source will always project a cyclically shifted version of the basic pattern, and correlating the detector image with the G decoding array will provide a sidelobe-free peak with position-invariant shape at the source position.
A source in the PCFOV will instead cast an incomplete pattern and its contribution cannot be a-priori subtracted and will produce secondary lobes (coding noise). On the other hand the modulated radiation from PC sources can be reconstructed by extending the correlation procedure, with a proper normalization, to the PCFOV.
URA masks also minimize the statistical errors of the reconstructed peaks. Since the variance associated with each reconstructed sky image pixel is constant in the FCFOV and equal to the total counts recorded by the detector; therefore the source signal to noise is simply
where and are source and background counts. These masks also have nearly equal number of transparent and opaque elements and therefore offer minimum statistical error in condition of high background (typical for the -ray domain). However the sensitivity also depends on the detector spatial resolution and an imaging efficiency factor must be applied to this maximum to account for this effect.
Discrete cross-correlation to compute sky and variance images can be written
where Poisson statistics was assumed. This standard deconvolution in FCFOV can be extended in the PCFOV by extending the correlation of the decoding array with the detector array in a non-cyclic form, padding with 0 elements. Since only the detector section modulated by the PC source is used to reconstruct the signal, the statistical error at the source position and significance of the ghost peaks are minimized. However to ensure a flat image in the absence of sources, detector pixels which for a given sky position correspond to opaque mask elements must be balanced before subtraction with the factor , where is the number of pixels corresponding to transparent elements and to opaque ones for that given sky position. This can be written
where the decoding arrays are obtained from the mask M by and , then padded with 0's outside mask region, and where the sum is performed over all detector elements. In the FCFOV we obtain the same result as the standard cross-correlation. To consider effects such as satellite drift corrections (see [7]), dead areas or other specific conditions, a weighting array is used to weigh properly the detector array before correlating it with the arrays. The balance array is
The variance, which is not constant outside the FCFOV, is computed accordingly
since the cross-terms vanish. Note however that when the weights refer to the same pixel in D, the terms must be summed before squaring (see [7]). The varying effective area can be calculated by a similar formula and used to renormalize, after background subtraction to FCFOV count rates. All this can be performed for sampling finer than 1 pixel per mask element and using a G array convolved with detector the PSF in order to optimize S/N for point sources, with corresponding normalizations. This procedure can be carried out with a fast algorithm by reducing previous formulae to a set of correlations computed by FFT.
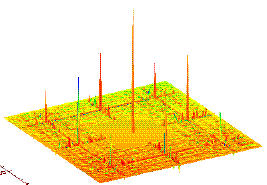
![[*]](crossref.png)
.
Note the peak and flat level in the central FCFOV,
the secondary lobes (coding noise) in the PCFOV
and the 8 main ghosts of the source peak in the PCFOV
located at distances, from the source, which are a multiple of the
basic pattern.
The average Point Source Location Error (PSLE) for an optimum coded aperture system with a defined SPSF depends on the source signal to noise ratio (S/N) as following
The IBIS/ISGRI telescope, assuming no error in pointing axis reconstruction or other systematic effects, can locate a 30 point-like source at better than 1 . Absolute error in attitude reconstruction for INTEGRAL is expected to be 20 .
In a standard analysis, IBIS events or histograms are binned in detector images, which are then corrected for detector and background non-uniformity [7] and then processed by an iterative algorithm which decodes, cleans and composes sky images. For each detector image a sky image and its variance are obtained using the deconvolution procedure, and then iteratively searched for sources and cleaned of the source side lobes. In this iterative process the source peaks are fitted with the bi-dimensional Gaussian and finely located. Then the source contribution to the image is modeled in detail and subtracted. The images are rotated, projected and summed after being weighted with the variance, and then searched for further contributions.
More details can be found in [8], [9]
